2の補数（2進数のマイナス表現）

--

--

✅動画解説はこちら！

#前提

まず、「２の補数」問題には前提ルールがあります。

①「bit長を定義して」表現することが決まっている
┗ 8bit =１Byte として、出題されることが多い。

②問題ごとに「符号付き」「符号なし」の前提が定義されている

#2進数のマイナス表現（数値感覚）

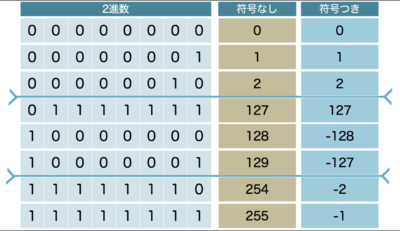
前提でもお話したように、２の補数問題では「符号なし」「符号つき」が問題文に記載されています。

そのため、2進数と10進数の数値は上記のようにかわってきます。

「符号付き」：＋ー表現　／　「符号なし」：＋表現のみ 

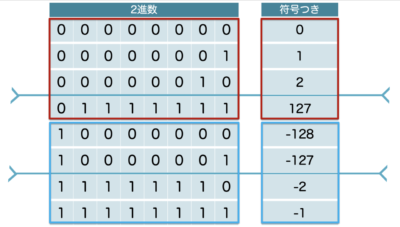
また、符号ありの場合は、最も大きい位の値が 0：正数：プラス / 1：負数：マイナス となるため

問題文の定義で「マイナスを2の補数で表す８ビットの数値」ときたら、この前提を覚えておくと、数値感覚がつかみやすいです。

#2の補数・変換方法

例題として、10進数の 116 → -116 のときの２進数を求めます。

求め方は下記の手順です。

✅ ０と１を反転させて、１を足す

計算方法は下記のとおりです。

2進数の世界では、 1 + 1 = 10 となるため、繰り上がるときも10進数の筆算と同様に計算しましょう。

#過去問を解いてみよう！

最後に過去問を解いてみましょう。

ブログ内での解説が難しかったので（すだれ算とか…）
動画内の ‘4分57秒〜’ で補完していただけると嬉しいです！