論理演算の基礎

--

--

✅動画解説はこちら！

# 論理演算とはなにか？

論理演算の「演算」とは、やっていることは「計算」と同じです。

計算と異なる部分は、扱う内容が数字ではなく、電気信号である点です。

そして、論理演算では、入力A,Bに対して、電気の流れを下記のように整理しています。

電気が流れている　→　真（True）：１

電気が流れていない　　→　偽（False）：0

# 論理演算の入出力のお作法

それでは、論理演算の基礎となる「演算方法（計算方法）」を学びましょう！

論理演算の真理値表は、暗記ではなく理屈で理解しましょう◎

はじめに、論理和と論理積の違いは、試験の合格基準の例から理解しましょう。

論理積（AND）

AND条件とは、「どちらの条件も満たす」という意味なので、ベン図は下記とおりです。

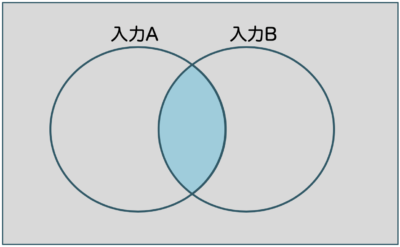
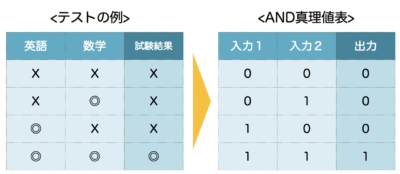
（例）英語と数学の両方が合格点なら、試験に受かる。

このときの結果は、下記のパターンになります。

（合格点→◎　／　不合格点→✗）

論理和（OR）

OR 条件とは、「どちらかを満たす」という意味なので、ベン図は下記のとおりです。

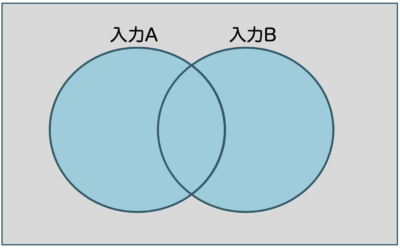
（例）英語と数学の片方が合格点なら、試験に受かる。

このときの結果は、下記のパターンになります。

（合格点→◎　／　不合格点→✗）

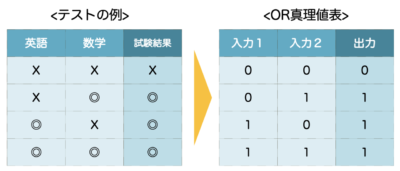
合格点（◎）を 1、不合格点（✗）を 0、と置き換えたとき、

入力値と出力値の関係は図の通りになります。

続いて、否定と排他的論理和は、先に解説した論理和と論理積の知識をベースに理解しましょう！

否定（NAND・NOR）

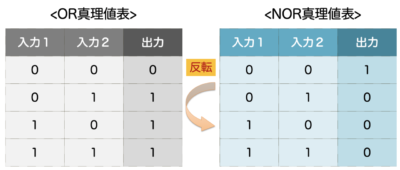
否定とは、ANDとORが反転した状態のことを指します。

頭につく”N”は否定の ‘not’ であることから、NANDは（not AND）、NORは（not OR）を意味します。

ANDとNAND

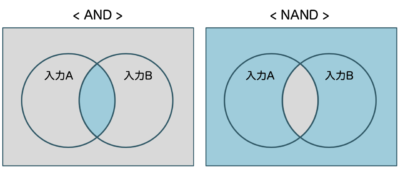
ORとNOR

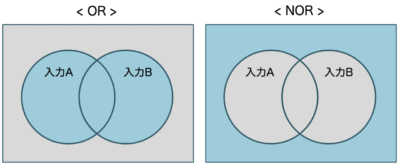
なので、入力値の表もANDとORの状態を反転させた次の通りになります。

・AND　→　NAND

・OR　→　NOR

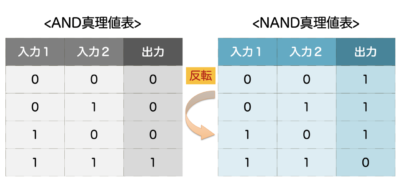
排他的論理和（XOR）

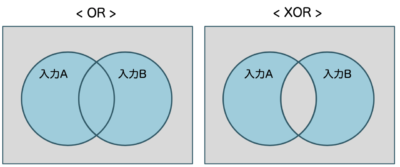
排他的論理和は、ORの重複部分を排除した図となります。

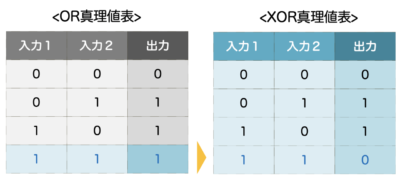
なので、入力値表も重複部分だけを反転させた結果が排他的論理和の特徴となります。

# MIL記号（ミル記号）の利用

MIL記号とは、論理演算を現実の回路図で表せるパーツのことです。

電気信号を送った結果を可視化することができます。

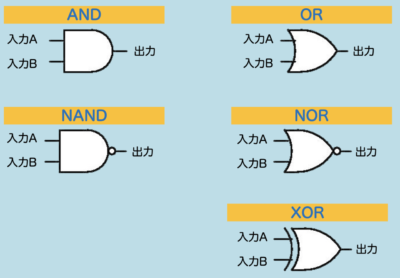
それぞれの条件時に入力A,Bに、どの値が入るかで出力結果がかわってきます。

コンピューターの世界は回路で出来ており、電気が流れる（1）、電気が流れていない（0）の２進数の世界で出来ています。

これらの組み合わせがIC（集積回路）です。

余談ですが、Twitterでこんなイラストを見つけました…

可愛すぎませんか😳

pic.twitter.com/z9LuH25Ovm

— Fuchur (@Vollplatsch) July 19, 2020

集積回路の事例

ここではもっともシンプルな半加算器について説明します。

半加算器の特徴は、1 bit 2進数（0,1）の1桁の足し算を扱うことが出来る装置のことです。

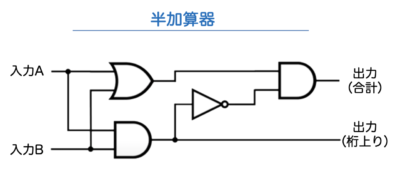
半加算器とは、論理積２個・論理和１個・否定１個、の組み合わせで作られています。

この半加算器で「1+1」を計算するときについて、論理演算の組み合わせ表に従って解いていきます。

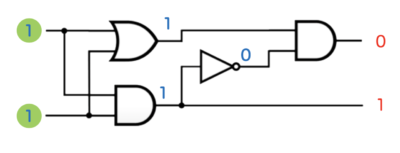
すると、1bit2進数の1+1 の答えは「10」となりました。

ちなみにこちらは「半加算器」であり、１桁の足し算しかできないことから
通常の足し算をおこなうときは「全加算器」といって、半加算器を組み合わせたものを使います。

いわゆる電卓の仕組みであり、電卓で計算できる桁数に上限があるように
加算器の組合わせに応じて、繰り上がりに対応可能なキャパも変わってきます。

関連記事