
--
--
✅動画解説はこちら!
今回は「n進小数」の回です。
ここでは、n進数で換算されたときの小数表現について学びます!
まずは、1011₍₂₎を10進数になおしてみましょう。
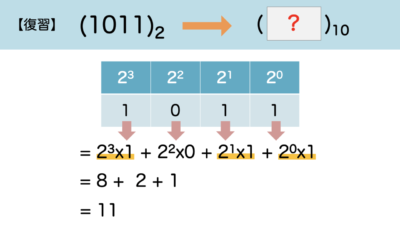
このように、1桁に2個数字が集まると位が一つ上がることから
各桁に何個ずつ数字が集まっているのか、分解して足してあげます。
それではさっそく今日のテーマ、2進数の小数を10進数に直すことから考えてみましょう。

この問題も、同じように、桁ごとに分解して計算してあげましょう。
さて、小数の指数表示を、みなさんは覚えていますか?
#私はうっかり忘れていました…
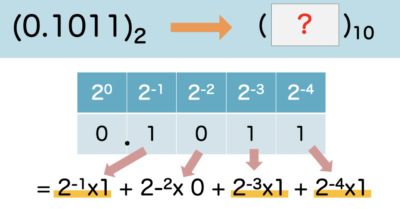
1の位が「0乗」で表されることから、0.1の位は、「マイナス1乗」と順に繰り下がって表記されます。
そのため、このように桁を整理することができました。

あとは、そのまま計算してあげることで成り立ちますね。0.6875が正解です。
計算のポイントは、2⁻¹ → 1/2¹ である点です。
10進数からn進数に変換するときの求め方は覚えていますか?
そうです、すだれ算でしたね!
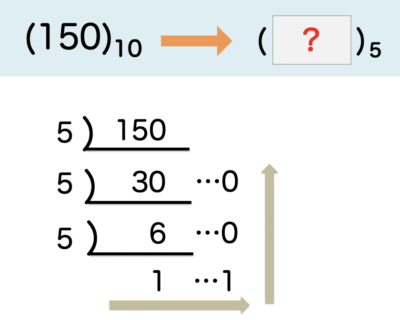
それでは、同じようにやってみましょう!

……あれれ、
同じように2ですだれ算をしようとすると
小数を2で割り続ける(2の塊が一つもない)状態となるので、うまく計算ができませんね。
なぜ「すだれ算」で求められるのか、立ち戻って考えましょう。
・整数のとき…2の塊が、求めたい数の中に、いくつ入っているか調べる
・小数のとき…2⁻¹(=1/2)の塊が、求めたい数の中に、いくつ入っているか調べる
なので考えてあげることは、求めたい数字(0.625)の中に、いくつ2⁻¹が入っているのか、
すだれ算は下記のように式を立ててあげましょう。
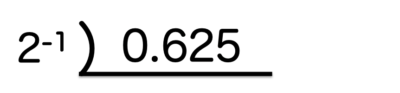
この計算方法となっても、0.625を 2⁻¹(=1/2) で割ってあげることに変わりません。
0.625を2⁻¹(=1/2)で割り算する、ということは、元の数字に2を掛け算してあげることと同じです。
また、元の数字に 2⁻¹(=1/2)がいくつ入っているかを知りたいため、
各数字に2⁻¹(=1/2)が何個入っているかを左側に記入・2⁻¹(=1/2)で割ったときの整数が個数、
となるため下記のように数字を整理しながら計算しましょう。
★ここは、動画のほうが分かりやすいです!
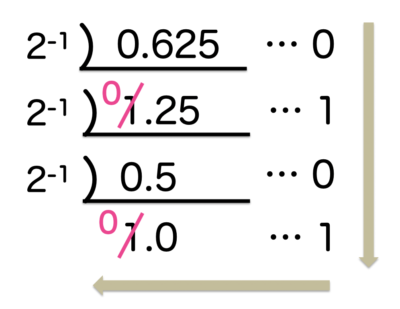
そして、2進数に落とすときも、上から読んで答えを導きます。
今回の場合は、0.1010が答えです。
最後に、n進数⇄n’進数で復習しましょう。

いつものごとく、10進数に置き換えてあげることで、求めましょう。
Aは、10進数でいうと「10」に該当するので、その前提で変換します。
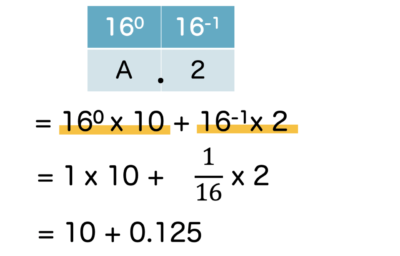
(A.2)₁₆は、(10.125)₁₀と示すことができるとわかりました。
続いて、(10.125)₁₀を2進数に変換する時は、すだれ算を整数部分と小数部分に分けて計算しましょう。

すると、整数部分は(1010)₂で、小数部分は(0.0010)₂となります。
整数部分と小数部分で、数字の読み上げ方が逆になることに注意!!
それぞれを足し上げると、答えは1010.0010となります。

ITすきま教室では講師や講演のご依頼もお受けしております。
YouTubeチャンネル運営のほか、ナレーターや司会業としても活動してきた経験から、分かりやすく満足度の高い講義をご提供します!



解説が分かりやすいと沢山の方からご好評をいただいており、IT資格勉強コンテンツで日本トップの登録者数を集めています。すきま時間を使って勉強して資格合格や成績アップを目指しましょう!
YoutubeチャンネルはこちらX(旧Twitter)で関連用語を3時間に1度つぶやきます!
すきま時間の学習にお役立てください!















